PART 8:  INFORMATION  SHEET  No. 6

BANDPASS  CIRCUITS

8.6.1   INTRODUCTION

The purpose and use of bandpass circuits was introduced in Part1, Lesson 10. This Information Sheet explores the underlying theory of their operation, the various methods of their implementation and details that will be useful to Constructors who would like to try designing and building their own. Such a task is much easier if you have equipment such as a sweep-oscillator and an oscilloscope but, as explained in the text, sophisticated equipment is not necessary to produce reasonable results; a hand-sweep with a normal signal-generator can serve well.

8.6.2   SIMPLE TUNED CIRCUIT

A single LC resonant-circuit produces a frequency-response of the kind shown in Fig.1 in which the response of the arrangement is shown as a function of frequency.

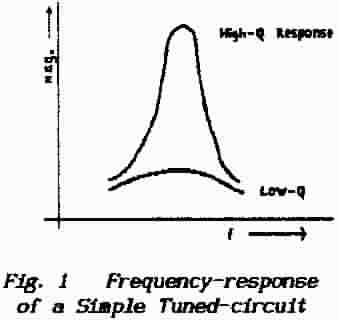For a so-called high-Q circuit the shape of this curve is very sharp and narrow and, at the peak-response frequency, it rises considerably above the out-of-band response. For a so-called low-Q circuit the curve is flat and broad and fails to rise appreciably above the out-of-band response. The high-Q circuit is useful in those amplifier arrangements where the response is required to be essentially at a single-frequency;  for example in an oscillator. The low-Q circuit is useful where the response is required to cover a range of frequencies as may be found in a radio receiver.

Fig.1 demonstrates the disadvantage of this simple arrangement in that, while the response of the low-Q circuit may be broad-band, it offers but little discrimination between the required in-band signals and undesired out-of-band signals;  i.e. its use results in both poor amplification and poor selectivity.

The behaviour of a resonant circuit as either high-Q or low-Q is determined by the amount of energy that the resonant circuit dissipates.   In technical terms by the losses or the damping that is present. This energy dissipation takes place of course in the components which make up that resonant circuit and so the circuit Q-factor is determined by the quality of the components from which it is constructed; i.e. by the individual component Q-factors (see Lesson 8 in Fundamentals-1). To manufacture components of poor quality is not a reasonable option because of considerations such as reliability and the need to maintain control over circuit behaviour. Thus the bandwidth of an LC resonant circuit is adjusted by adding a known amount of loss in the form of a damping resistor.

It is evident from the foregoing discussion that a broad-band response and high-gain are not compatible and so an alternative to the simple resonant circuit is required.

8.6.3   COUPLED-CIRCUIT THEORY

Broadband responses are obtained by coupling together several simple LC-circuits.   There are several methods of achieving such coupling but perhaps the easiest to grasp is that which uses the transformer principle.

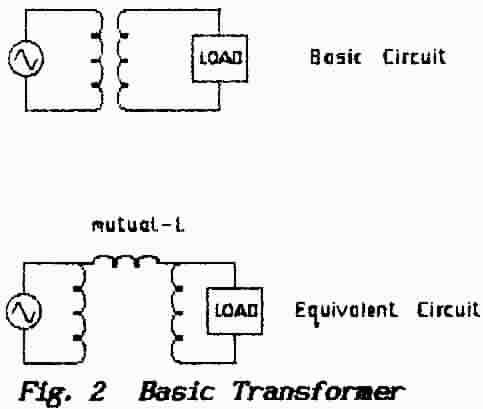Fig. 2 shows a basic transformer. The exact mechanism whereby energy is transferred from the primary circuit to the secondary circuit is not known but it is known that the amplitude of the secondary signal is dependent on the rate at which the primary current changes. At the peaks of the primary-current waveform the current is reversing sign either from positive-going to negative-going or from negative-going to positive-going and so, at these points, the rate-of-change is zero.

Midway between the peaks where the waveform is crossing the zero line the rate-of-change reaches a maximum value. 

From this can be deduced that the peaks of the secondary waveform coincide with the zero-crossings of the primary current and that the zero-crossings of the secondary waveform coincide with the peaks of the primary current;   in technical terms there is a 90° phase-difference between primary and secondary waveforms.

This phenomenon can be interpreted by saying that the transfer characteristic (i.e. a comparison of the output-signal with the input-signal) has the characteristic of a Reactor — there is a 90° shift in phase as the signal transfers between the transformer windings.   The argument is the same which ever winding is designated as the primary and so we say that the windings are mutually coupled.   In fact the inter-winding coupling behaves as though it were an inductor and so it it always represented as a mutual inductance.

The magnetic field produced by the primary current does not entirely couple with the secondary winding of a transformer:  a proportion of the field fails to do so and this is referred to as magnetic leakage.  Leakage is expressed as a coupling factor which is given the symbol k.   Should k = 1 then the leakage is zero;  if (say) k = 0. 85 it signifies that only 85% of the magnetic field is linking with the secondary and as a result the signal coupled into the secondary circuit is 85% of that otherwise to be expected.

The same argument can be applied to the secondary current and the manner in which it couples to the primary circuit.

This is a simplified (not entirely accurate) account of transformer behaviour but it serves to demonstrate that primary and secondary signals are not identical in Time.  Standard textbooks will be delighted to present a detailed analysis of transformer action in terms of a vector-diagram and one quick look at that will explain why I do not give such an account here.   This inherent phase-shift caused by the inter-winding magnetic-coupling produces some rather odd (but useful) results.

If the Load shown in Fig.2 is a pure resistor then the Generator, “looking- in” through the transformer input-terminals, sees a resistive load shunted by the inductive-reactance of the transformer windings.  The aim in transformer design is to ensure that this inductive-reactance has a very-high value at the working frequency and so it can be ignored in this discussion.

If however the Load consists of a capacitor then the Generator sees an inductive-reactance while, if the load is an inductor, then the Generator sees a capacitive-reactance.

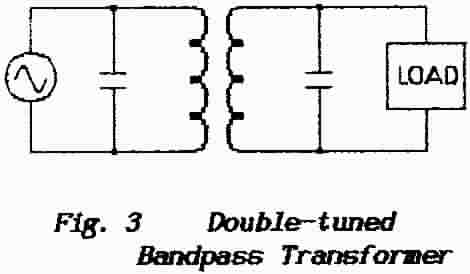Fig. 3 shows a Generator coupled to a Load via a double-tuned transformer;  this basic arrangement is to be found in most receivers. Both primary and secondary windings are adjusted to resonate at the same frequency (the method of achieving this is dealt with later). The frequency of resonance is defined as that frequency at which the inductive reactance is equal to the capacitive reactance;  the two reactances cancel so leaving both primary and secondary windings purely resistive in nature.  However, it must still be true that the primary and secondary currents are, relative to each other,  phase-shifted through 90-degrees and so transformer action as described above is to be expected.

An Observer who “looks into the primary circuit” in place of the Generator would see the Load coupled through the transformer action; the Observer who“looks into the secondary circuit” in place of the Load would see the Generator coupled through the transformer action.

(a)  Frequency Too Low     When the frequency of the generator is lower than the resonance frequency then the inductive-reactances (in both circuits) fall and the capacitive-reactances rise;  as a result the behaviour of each circuit is controlled by the capacitive reactance and we say that the circuit becomes predominantly capacitive. With reference to the previous paragraphs the Generator is presented with a primary circuit which has a capacitive-impedance plus a coupled secondary circuit which has been transformed to an inductive-impedance.  Similarly the Load, looking back toward the Generator, is being driven by a secondary circuit with a capacitive-impedance plus a coupled primary circuit which has been transformed to an inductive-impedance.

For both primary and secondary windings the change of impedance (from resistive to capacitive) is modified because the coupled impedance from the other winding appears to be inductive.   Hence the departure from resonance which might be expected because of the change of frequency tends to be compensated.

(b)  Frequency Too High     The same argument applies when the Generator frequency is raised above that of resonance.  Both primary and secondary circuits become inductive but each couples into the other a capacitive impedance which tends to compensate the overall impedance change caused by frequency changes.

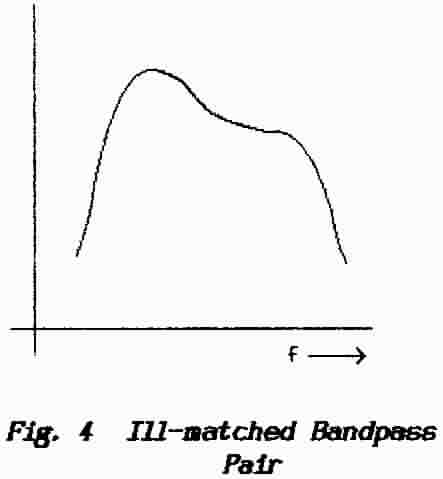The double-tuned arrangement shown in Fig.3 thus tends to remain “in tune” over a short range either side of the frequency to which the two circuits are resonated.   The extent to which this self-compensation is successful depends on how well the two circuits are matched.  They must have the same Q-factor and be tuned to the same centre-frequency;  the result of failure in this respect is shown in Fig. 4. The bandpass effect depends too on the degree of coupling.   It should be obvious that, if the coupling is too small (i.e. the two circuits are not coupled), then signal transfer from the Generator to the Load will not take place.

As the coupling is increased so the signal level at the load will rise steadily accompanied by a similar increase in the frequency compensation. It is possible to make the coupling too tight so that the circuits are over-compensated;  when this happens the circuits are de-tuned off-resonance instead of offering mutual-compensation.

The result of varying the coupling is shown in Fig. 5. Between the under-coupled single-peak response and the over-coupled double-peak response there is a happy mean in which the circuit response remains substantially constant over a range of frequencies.   This “flat-topped” condition is termed critical coupling.

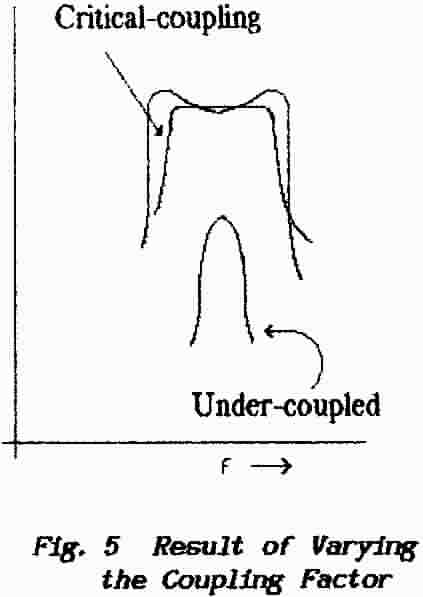It is usual to employ a coupling factor which is slightly greater than the critical value and this is indicated by the appearance of two small maxima in the frequency response as shown in Fig.5. The amplitude of these bumps is under control as the coupling is increased;   the advantage of this condition is that the bandwidth achieved is slightly greater than that at critical coupling and also that the skirts of the characteristic are considerably steeper than with critical coupling.

8.6.4   OTHER FORMS OF COUPLED-CIRCUIT

The double-tuned--transformer introduced above is but one way of coupling two resonant circuits.   In the equivalent circuit of Fig.2 two resonant circuits are shown coupled by a mutual-inductance but this can be reproduced by using any form of reactance that is common to both circuits;  indeed any common impedance will suffice through which the interchange of energy can take place.   Four alternative arrangements are shown in Fig. 6.

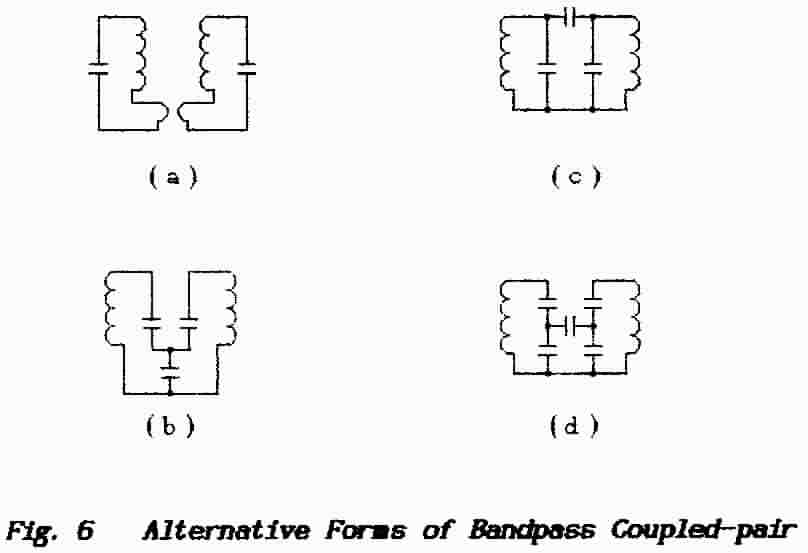
Diagram (a) shows an alternative form of the transformer-coupling illustrated in Fig.3;  this type of circuit was once common in valve-operated communications receivers where it played a part in arranging for variable bandwidth in the IF amplifier. Yet another variation occurs where the “transformer” is replaced by a low-impedance untuned link-coupling thus allowing the two resonant circuits to be physically separated.

To set-up an inductively-coupled pair they must first be separated so as to reduce the coupling;  when each circuit has been tuned for maximum response at the desired centre-frequency (f_c) then the coils are moved closer together until the required bandpass characteristic is obtained.   The two coils are then cemented to hold them in position.

Should re-adjustment be necessary it may not be possible to release the cement and then a different technique is employed. Each circuit in turn is shunted by a low-value resistor to lower its Q after which the other circuit can be tuned. However the coupling-factor can only be changed by moving (one of) the coils.

Diagram (b) shows much the same arrangement but this time each resonant circuit is tapped in the capacitive arm instead of in the inductive arm. Here the resonance frequency is determined by Cl and C2 in series while the coupling-factor is determined by the ratio C₂/(C₁+ C₂).   A difficulty here lies in adjusting the circuit;   adjustments to the tuning or to the coupling are inter-dependent.

Diagram (c) shows a capacitive form of the circuit illustrated in Fig.2 in which the mutual-inductance-coupling is replaced by a coupling capacitor;  sometimes the required value of this capacitor is impractically small and so the component is “tapped-down” the circuit as shown in diagram (d). As the tapping-point is moved down so the circuit impedance at the tap is reduced and thus the required value of the coupling capacitor is increased. This arrangement can be realised also by tapping down the inductive branches but it is generally easier to divide the capacitive arm than it is to arrange for tapings on the coils.

Whether the circuits are tapped in the inductive arm or in the capacitive arm the same rule applies as for transformer action; the impedance-ratio is proportional to the square of the turns-ratio or to the square of the capacitance-ratio.

This arrangement is very easy to set up because the coupling capacitor can be variable. It is set for minimum capacitance (highest impedance and smallest coupling-factor) and then the two resonant circuits can be individually tuned to the centre frequency. The coupling-capacitor is then increased in value until the required band-pass characteristic is obtained.

8.6.5   TO DESIGN A BANDPASS COUPLED-PAIR

As explained in the Lesson notes bandwidth is related to the Q of a circuit which broadly is the Q of the inductor;  this is defined as the ratio Rp / Xp, where Rp is the parallel-connected resistance (the losses) of the circuit.

These circuits are adjusted to be resonant at the centre frequency and so the value used for X may be that of the inductive-reactance or of the capacitive-reactance. The following formula relates Bandwidth (ß) in Hz to the values of capacitance (C in Farads) and resistance (R in ohms) with reference to the circuit shown in Fig. 7:

ß  =  √2 / (2π.√C₁C₂.√R₁R₂

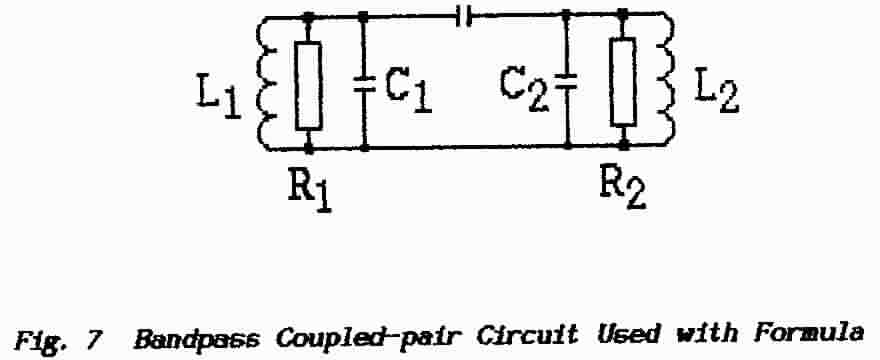
In fact the formula relates to any type of coupled-pair arrangement.  It has been said that an essential feature for a flat-topped characteristic is that the two coupled-circuits be well matched ;  it follows that C₁ =  C₂ and  R₁ =  R₂ and so the formula reduces to

ß = √2 / 2πCR

Compare this with the formula for a single tuned circuit in which ß  =   f₀ /Q  =   l / 2πCR

There is a minor catch however in that the values calculated for both C and R represent the total effective capacitance and resistance in each circuit;  this means that C is formed by the combination of the lumped capacitor and stray-capacitances and that R is formed by the combination of the lumped resistor and inherent losses.

The value of C is easily disposed of because the added capacitor has to be (or to include) an adjustable trimmer. The value required for the additional resistance however depends on the measured value of the circuit losses;  to determine this either

(i) the coil must be wound, adjusted for approximately the correct value of inductance and then measured on an Admittance Bridge to find the value of Rp.  The value of the added resistor must then be calculated to produce, in parallel with the measured value, the required value of Rp in the above formula

(ii) When a Bridge is not available then the value of R as calculated must be increased by guesswork and adjusted so as to achieve the designed Bandwidth when the circuit is finally set-up.

The flat-topped characteristic depends on the coupling between the two resonant circuits achieving the critical value. This coupling-factor k is determined from the formula

k  =  ß/fo  =  Cc/C

An important parameter when designing a bandpass amplifier is the load which the coupled pair presents to the active device. This value is the parallel resistance of R₁ and R_2.    Thus, in the design of an IF amplifier, the first step is to determine the desired value of the load and then R₁ and R₂ are each assigned twice this required value.  Note however that R₂ may have to be increased in value because it will be shunted by the input-resistance of any following stage.

END OF INFORMATION SHEET 6