PART 7:  MATHEMATICS  FOR  AMATEUR  RADIO

LESSON  7

7.7   THE  j-NOTATION

7. 7. 1 General

      The j notation is a mathematical tool whose purpose is to prevent confusion between two sets of figures which relate to different types of quantities.  Mathematicians use the letter "i" but, in electrical engineering, that letter has other connotations.

7.7.2  Derivation of j

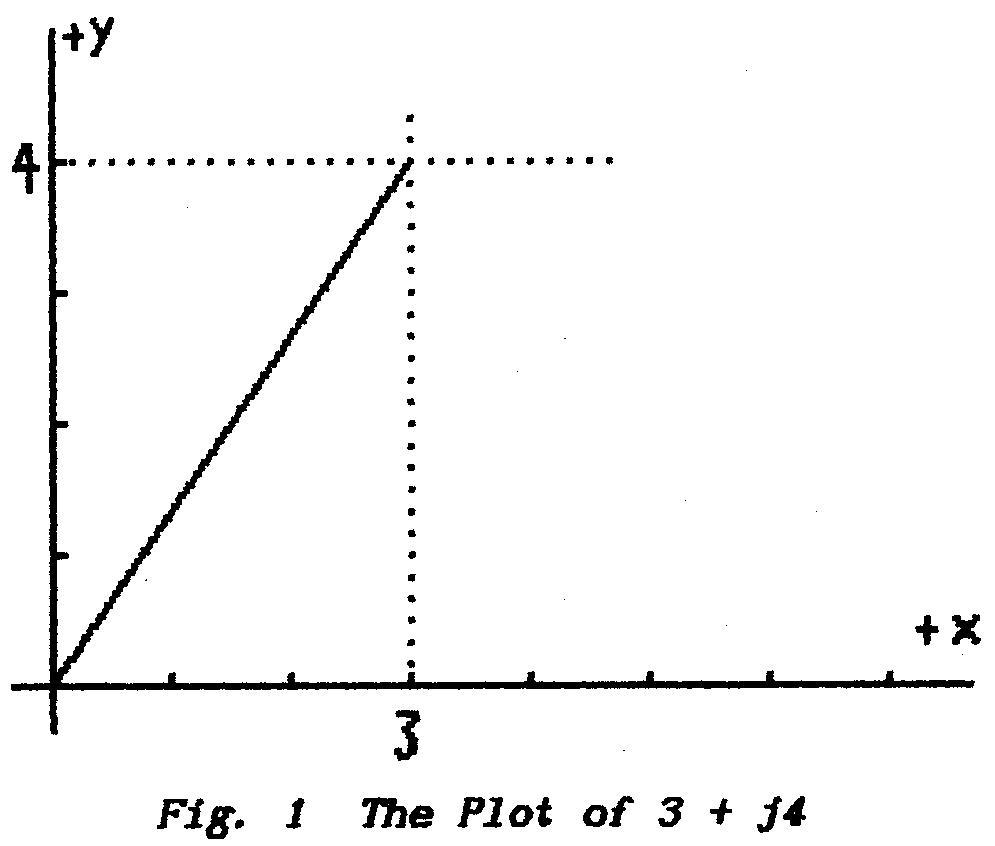Fig. 1 shows two axes which, by representing two different quantities, are used for plotting graphs as described in Lesson-3 of this Part.  To be more accurate Fig. 1 shows only that part of each axis which lies in the first quadrant; i.e. only the positive values of an independent-variable x (horizontal axis where x may have any value) and only the positive values of the dependent-variable y (vertical axis where the value of y depends on the value of x). As discussed in Lesson-3 a particular point in this diagram might be designated as 3,4 meaning that x = 3 while y = 4. The point is plotted in Fig. 1 at the intersection of a vertical line which passes through x = 3 and a horizontal line drawn through y = 4. Carry out such an exercise and you will find that, as predicted by Pythagoras' Theorem, the plotted point lies at a distance of 5 units from the Origin.

This diagram shows one instance where simple arithmetical addition of the values of x and y does not yield the correct answer  namely, in this instance, 3 + 4 = 5 . The reason is that x was measured from 0 in a horizontal direction while y was measured from 0 in a vertical direction while the distance from point 0 to the plotted point is measured in yet another direction.

To indicate that these two numbers cannot be added except under a set of special rules the letter j is placed before one of them.  Numbers represented by the length of the horizontal axis are referred to as real numbers and are written normally.  Numbers represented by the length of the vertical axis are known as imaginary numbers and are written with the letter j before them. Thus this particular plotted point can be described as being at a distance 3 + j4 from 0.

Because the two axes are set at 90⁰ the result of this vector addition can be calculated using Pythagoras' Theorem which applies to any right-angled triangle namely that the length of the resulting line is given by:

√(3² + 4²)  = √(9+ 16)  =  5.

However j can be more useful than just an indicator of quantities which cannot be mixed. It can be used as an Operator which is a mathematical tool such as + or - .   Its use as an Operator is derived as follows:

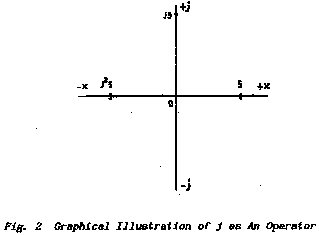
Fig. 2 shows the two axes complete with both negative and positive values.  Along the x (horizontal) axis positive numbers are represented as line-lengths measured to the right starting from the Origin. Similarly negative numbers are represented as line-lengths measured to the left starting from the Origin.

Under the rules of arithmetic:

(a)     a positive number becomes a negative number when it is multiplied by -1

(b)     a negative number becomes a positive number when it is multiplied by -1

This can be represented on Fig.2 by regarding a multiplication by -1 as a 180⁰ rotation about the Origin "0".  A second such rotation (another multiplication by -1) returns the plotted point through a total of 360^o to its original position.

Now consider the imaginary axis on which quantities jy are plotted.  The same argument must be applied of course and so multiplication of imaginary numbers by -1 must also be regarded as a rotation of 180^o..

Now that Fig.2 has been constructed under these rules a small query arises:

a quantity (for example 5) plotted on the horizontal axis is moved to the vertical axis when a j is placed in front so that it becomes j5.   By direct analogy, if multiplying by -1 rotates +5 through 180^o to position -5 then does not placing a j before it amount to multiplying that quantity by j so causing a rotation through 90⁰?

This isn't really a fiddle;  the diagram was constructed under given Rules and, if the diagram is to be valid, the Rules must always be observed. From the Rules the idea arises naturally that an imaginary quantity is to be regarded as a real quantity multiplied by the Operator j.  Similarly a real quantity has to be regarded as an imaginary quantity multiplied by the Operator j.

Now there is one last step.  Multiplication twice by the Operator j (two rotations through 90⁰ ) clearly leads to a rotation of 180⁰ already defined as multiplication by -1.    In other words

 j²   =   -1

which leads to the embarrassing statement that

j  =  √(-1)

The Rules of mathematics say that minus x minus equals plus and also that plus x plus equals plus and so there cannot be any number which, multiplied by itself, equals -1?

You are entitled to deduce from this, if only because it is true, that j cannot have a numerical value. However it does not necessarily follow that the result is useless.

7. 7. 3   Use of j as an Operator

As an Operator the symbol j changes a real quantity into an imaginary one or an Imaginary quantity into a real one. That, under these Rules, j represents the square-root of -1 is useful when solving problems in Algebra.

Consider for example an inductance in the primary circuit of a transformer.  Measured in the secondary winding this inductance appears as a capacitance because of the phase-shift that takes place as a signal passes between the windings. (This effect is utilised to provide frequency-correction in bandpass coupled-circuits (see under 3.13.4).    In a theoretical analysis of the transformer the reactance (a  j-term) in the  primary becomes multiplied by a second j-term which represents the phase shift between windings;  the resulting term contains j²  ( =  -1) which  indicates that, in passing between the transformer windings, an inductive reactance is transformed into a capacitive reactance (true);  similarly a  capacitive reactance is transformed into an inductive reactance.

During the course of algebraic manipulations the principle is taken further and the unwary can fall into some nasty traps.  Thus

 j³   =  j x j²   =   j  x -1  =  -j

and

j⁴ = j² x  j²  = -l  x -1  =  1

NOTE These values for j do not have any arithmetical meaning;  they are used only in evaluating algebraic results in terms of Fig.2.

In Fundamentals-1, Lesson-8  it was simply stated that the impedance (Z) of a circuit represented by (R + jX) is found by squaring the two quantities R & X, adding the results and then finding the square-root of that sum ;   in symbols

Z  =  √(R² + X²)

That formula also expresses the result of Pythagoras' Theorem which relates the sides of any right-angled triangle. The use of  j  to describe two quantities represented as right-angled vectors is based therefore on the solution of  Pythagoras' Theorem.

This derivation of Z is only valid of course provided that R & X are truly at right-angles;  i.e. that the values refer to "pure" or theoretically perfect components in which the current and voltage waveforms are exactly phase-shifted by 90⁰.   This does not raise a problem of course because practical components are regarded as being pure components degraded by a resistor (representing losses) connected either in series or in parallel with that component.

The assumption is always true because practical values of L, C & R can be obtained only by making measurements and, in making these,  it is assumed that the lack of purity is caused by a (theoretical) resistor connected in one of these configurations.

END OF LESSON