
Trigonometry is the branch of mathematics which studies the properties of triangles. On a higher level Geometry is the study of space (i.e. of shapes) and this deals in:
(a) one dimensional lines which are expressed in Linear Measure or units of length (L)
(b) two-dimensional plane figures which are expressed in Square Measure or units of area (L2)
(c) three-dimensional solid figures which are expressed in Cubic Measure or units of volume (L3)
The triangle is the simplest of the Plane Figures. Given three points they can describe only a triangular plane and that is why a three-legged stool, table or any form of tripod will always stand firmly (it will always find a plane surface) whatever the terrain even if the legs are not all of equal length. Given four points the resulting figure could be a plane (a rectangle) but, most probably the result would be the solid form - a triangular pyramid.
A triangle is described also by three intersecting lines, known as the sides of the triangle, and the three points of intersection are the three points mentioned above. These three points are known as the apeces of the triangle (the plural of apex.)
In turn these three sides define three angles which are the shapes enclosed where two lines (or two planes) intersect. To get to grips with angles it is necessary to consider a unique plane figure the circle which is a special form of the more general ellipse.
On first acquaintance the circle is an uninteresting beast with but three parameters namely:
(i) a point which defines the centre of the circle and which usually is labeled "O".
(ii) a circumference which is a line that defines the circle and which is at all points a constant distance from the centre.
(iii) a radius which is the distance from the centre to the circumference and which usually is labeled "r". A line drawn right across a circle and which passes trough the centre contains two such radii and is known as the diameter "d".
(The Geometry theorems of Euclid show that the circle possesses hidden depths).
Stand at the centre of a circle and look due North and it is possible to rotate to the left (without moving from the centre point) and to continue the rotation until you once more look due North. At the end of this manoeuvre one whole circle of rotation has been completed; in mathematics it is accepted practice to make all such measurements in an anticlockwise direction which is why rotation to the left was specified. (Measurements made in a clockwise direction are given negative values).
Should this rotation be abandoned before the full circle has been completed some method of describing the stopping point is required. For this purpose the full circle is divided into 360 degrees (written 360°); the name is derived from a Latin word which means "step". An angle describes a change in direction, or the difference in directions of the two lines which define that angle; if the point of intersection is taken as the centre of a circle then the angle can be measured in degrees. Such measurements are referred to as angular measure or circular measure.
For a circle with a small diameter a degree represents a short distance around its circumference; for larger circles the degree may be sub-divided into 60 minutes (written as say 40') each of which is sub-divided into 60 seconds (written say as 30") and these are referred to as minutes of arc and as seconds of arc.
There is a second method of measuring angles and, in electrical engineering, this method has advantages if only because it simplifies mathematical expressions and operations. If the diameter of a circle is marked off along the curve of its circumference it is found that it fails to divide that circumference into a whole number of parts. Whatever the size (the diameter) of the circle it is found that the result of dividing its circumference by a diameter always yields the same number — and that number is a very awkward one indeed.
The exact value of this ratio is not known even though it has been calculated to many decimal places on computers; because it is not an exact number it is referred to by the Greek letter π (pronounced pie and written "pi"). It has the approximate value 22/7 or, more accurately 3.14159.
Fig.1 shows a circle with its centre at a point O. Two different radii of length r are shown one drawn from O to a point A and the other drawn from O to a point B. The distance from A to B measured along the circumference is also of length r. The angle defined by these two radii - the angle which is subtended by the arc AB (where AB = r) - is defined as one Radian.

Because the circumference of any circle can be divided by the diameter π times it follows that the circumference can be divided by its radius (equal to half a diameter) 2π times. Hence rotation through a full circle (360°) represents a rotation through 2π radians; a half-circle (180°) is equivalent to π radians; a quarter-circle (90°) is equivalent to π/2 radians (read as pi-by-two).
The quarter-cycle of 90° or π/2 radians is referred to as a right-angle because, if one side of the angle is regarded as a base, then the other side stands "right" (or upright). Trigonometry is based on the remarkable properties of triangles in which one angle is a right-angle.
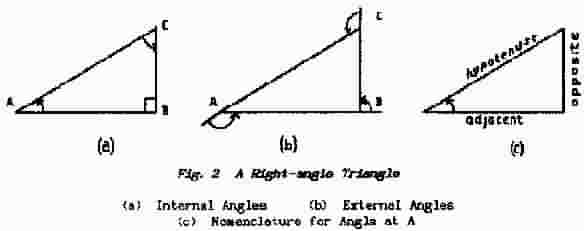
Fig. 2 shows a right-angle triangle ABC with the right-angle at B. In diagram (a) only the internal angles are shown. In diagram (b) the so-cal1ed external angles are shown; these still lie between the sides but they are external to the triangle. Although the triangle shown is a right-angle triangle the following arguments can be applied in general to any triangle.
Imagine that ABC is a large triangle and that you are able to walk along its sides. Start at A, look toward C and walk from A to C. At C rotate positively (anticlockwise) until you are able to walk backward toward B. At B again rotate anticlockwise until you are able to walk forward toward A. Now rotate anticlockwise for the third time until once more aligned with AC. Note that you now face toward A although the exercise began facing toward C; i.e. in negotiating the three internal angles of a triangle a rotation of only 180° (or π radians) has been necessary. This is one way of deducing that the three internal angles of any triangle sum to 180°.
To repeat the exercise on the three external angles start again at A but walk to B where an anticlockwise rotation leaves you able to walk (forward) to C. At C another anticlockwise rotation makes it possible to walk forward to A where the third anticlockwise rotation leaves you again facing toward B. This time a full circle of rotation has been necessary and so the three external angles of any triangle sum to 360° (or 2π radians).
If the three internal angles sum to 180° and the angle ABC is a right-angle (90°) then the two internal angles BAC and BCA must always sum to 90°; the two angles are said to be complementary (NOT complimentary). Thus, once a value has been assigned to any angle BAC the value of the third angle BCA is fixed.
It is found also that, in a right-angle triangle, once a value is given to one of the non-right-angles. the ratios of any two sides is fixed irrespective of the size of that triangle. With three sides involved there are three possible pairings and, for trigonometrical purposes, the actual ratios for each of those pairings have been calculated and tabulated against all possible values of angle. Given minimum information about the values of either any two sides or one side plus one associated angle it is possible to calculate a complete solution for any right-angle triangle.
The nomenclature used in Trigonometry is designed to give positive identification of the sides and angles of any right-angle triangle as shown in Fig.2 (c);
(i) the side opposite the right-angle is called the hypotenuse (pronounced high-pot-en-youse) and this is side AC
(ii) the angle under consideration is included between the hypotenuse and its adjacent side; for angle BAC the adjacent side is BA while for angle BCA the adjacent side is BC
(iii) the remaining side, the side which is opposite the angle under consideration, is called the opposite side
Note that the adjacent side for one of the complementary angles is also the opposite side for its complement (the other angle that brings their sum up to 90°).
There are three main ratios which are tabulated and they are defined as:
sine the ratio opposite/hypotenuse written as sin
cosine the ratio adjacent/hypotenuse written as cos
tangent the ratio opposite/adjacent written as tan
Those familiar with algebraic division will see that dividing sin by cos yields tan
Although a book of Tables contains other trigonometrical ratios the above set are the basis of them all. Three other ratios are merely the inverse of the basic ratios:
secant 1/cosine hypotenuse/adjacent written as sec
cosecant 1/sine hypotenuse/opposite written as cosec
cotangent 1/tangent adjacent/hypotenuse written as cot
The purpose of those last three tabulations is simply to save time and effort when a mathematical expression calls for an inverse ratio.
Another set of tabulations are labeled Logarithmic Sines (written as logsin), Logarithmic Cosines (written as logcos) and Logarithmic Tangents (written as logtan). Today when calculators are available these Tables are seldom used but the purpose of these last three was once again to save time and effort in evaluating expressions such as a.sinθ (where a is a number and θ is an angle); multiplication of the two would involve first looking-up the sine of angle θ and then finding its logarithm from the Log Tables. A Logsine Table enables a direct step between the va1ue of the angle and the log of its sine.
To try to learn all these ratios and derivatives usually leads to confusion; it is best to remember say only the sine (opp/hyp) and that the cosine is “the other one”. Tangent does not involve the hypotenuse and there is also the useful relation that sin/cos = tan.
The use of this Table is very straightforward. Suppose that side AB in Fig. 2 is given as 10cm in length and that angle BAC is 30°. To solve the triangle the first step is to deduce that the third angle BCA has the value
90 - 30 = 60°.
Side AC is calculated either from the cosine expression or from the sine expression as
AC = adjacent/cos30° or as AC = opposite/sin60°
= 11.547 cm
Either of these equations could have been simplified by using the inverse ratios such as
AC = adjacent x sec30°
Because of the complementary nature of the two angles it is possible to combine sin and cos in a single Table and also cosec and sec in a single Table. To read sines enter with the angle in the left-hand column and move into the columns on the right for partial degrees as indicated along the top line. To read cosines enter with the angle in the right hand column and move into the columns to the left for partial degrees as indicated along the bottom line. The last columns on the far right are given as an aid when interpolating between columns; they represent the differences from one column to the next.
In the example given above the third side BC can be calculated in the same way. However because this is a right-angle triangle, there is an alternative method which is sometimes useful in the form of Pythagoras' Theorem which states that (with reference to Fig.2)
AC2 = AB2 + BC2
The presence of the squared terms suggests that this formula is concerned with square-measure or areas and indeed this is the basis of the proof first deduced by Pythagoras; he showed that the area of the square constructed on the hypotenuse is equal to the sum of the areas of squares constructed on the other two sides.
Thus the required third side BC is given by √(AC2 - AB2). It is sometimes easier to use this expression when the sides of the triangle are whole numbers. Some values are worth remembering; for example side-lengths of 3, 4 & 5 satisfy Pythagoras' Theorem - can you find any other sets of whole numbers.
Notes
The sample Tables attached to this lesson are known as Four-figure Tables and they provide accuracy to three decimal places. For greater accuracy Seven-figure Tables are used - often found in sets of Navigation Tables. However it is easy to achieve accuracies up to 12 decimal places with computers and some calculators.
The term "circular measure" is generally used in Tables to indicate the measurement of angles in radians.
Conversion between degrees and radians is achieved by starting with a full circle of 360° and 2π radians.
When converting from radians to degrees the value is larger in degrees than it was in radians hence multiply by 360 and divide by 2π (x 180/π).
When converting from degrees to radians the value is smaller in radians than it is in degrees; hence multiply by 2π and divide by 360 (x π/180).
The paragraphs above show how a right-angle triangle can be solved using trigonometrical tables provided that either two sides are known or one side and an angle. The definitions of sin, cos and tan relate specifically to right-angle triangles but the technique can be used to solve triangles which do not include a right angle.
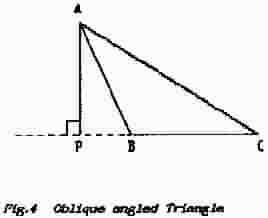
Fig. 3 shows such a triangle in which a perpendicular (a line at 90°} has been dropped from one apex of the triangle to the opposite side; the name indicates that the construction line has been drawn so that it divides the parent triangle into two right-angled triangles.

It is now possible to solve both of these component triangles using sin, cos or tan ratios, so evaluating the sides and angles of the parent triangle provided of course that the requisite minimum information is available. The significant fact is that the constructed perpendicular is common to both triangles; if either of them can be solved then the common side enables the calculation to be transferred to the other triangle in which is now known a side and one of the angles.
By using purely algebraic techniques on this problem it is possible to produce formulae which relate the sides and angles of the parent triangle; the usual nomenclature, a kind of shorthand, is shown in Fig.3(b) wherein the side opposite the angle at A is named "a" while the angle itself is named "A". The solution of such triangles is not required for the R.A.E. and the matter is not pursued here but the appropriate formulae can be found in any mathematical or electrical reference book.
Relaxation of the requirement for one angle to be 90° gives rise to the possibility of two different types of triangle:
(a) a triangle in which all the angles are 1ess than 90° as shown in Fig. 3
(b) a triangle in which one angle is greater than 90° and which is known as an oblique-angled triangle as shown in Fig.4 .
 |
To solve an oblique-angle triangle a similar construction is used namely a perpendicular is dropped from the apex A on to the base CB extended. The term hypotenuse can still be used for the side opposite the right-angle but the remaining two names "adjacent" and "opposite" become confusing. By definition the side AB is the side opposite angle ACB but the sin and tan ratios for that angle involve the constructed perpendicular AP; for this reason the word "perpendicular" is often used in place of "opposite". |
Similarly the adjacent side is really CB and not CP but this is not likely to cause confusion; thus for angle ACB the three ratios become:
sin ACB = perp/hyp = AP/AC
cosACB = adj/hyp = CP/AC
tanACB = perp/adj = AP/CP
WARNING To find the corresponding ratios for angle BAC it is necessary to make a new construction by dropping a second perpendicular from C to AB extended.
For a non-right-angle triangle the terms "opposite side" and "adjacent side" do not refer to the sides of the triangle and angles such as PAC are not an internal angle of the triangle.
The same construction is used to find the sin/cos/tan ratios of a triangle's external angles. In Fig.4 for example the sine of external angle ABP is AP/AB and this is also the ratio for the internal angle ABC. If this treatment of angles greater than 90° seems a bit obscure or casual the following derivation may perhaps clarify the matter.
In Fig.5(a) angle A2OA1 is created by rotating a line OA from the starting position OA1 to the position OA2; let the angle traced out be called θ (the Greek letter theta). To find the sin/cos/tan ratios of angle θ it is necessary to drop a perpendicular from A2 to the base-line OA which it intersects at point P.
When θ is zero the points A2 and A1 are coincident, point P lies on top of them, the perpendicular has zero length and the adjacent side is equal in length to OA. As θ increases from zero toward 90° so AP begins to increase and OP decreases until, when θ = 90°, the perpendicular is equal to 0A and the adjacent side has zero length.
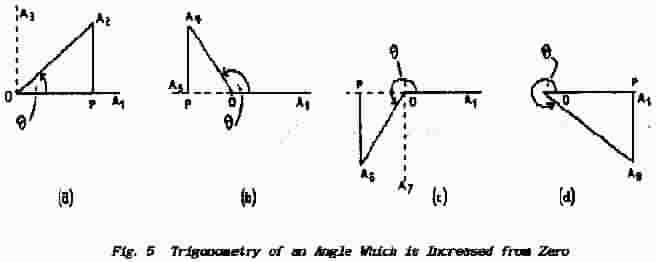
Further rotation of 0A beyond 90° creates the oblique-ang1e triangle A4OA1 in which the angle of interest - the angle being created by the rotation of OA - is the oblique angle A4OA1. The perpendicular AP is carried beyond the base line A1P and, as θ increases from 90° to 180°, so AP decreases toward zero and 0P increases toward the length 0A in the position 0A5. This is shown in diagram (b).
It must be noted however that 0A was measured to the right starting from the origin at 0 while 0A5. is measured to the left; if movement of P from A1 to O is a steady decrease in length then its further travel from 0 to A5 must be considered a further decrease in length and so the length 0A5 must be a negative quantity.
Still further rotation of 0A beyond 180° is shown in diagram (c) and it leads to the creation of the angle A6OA1. Once again the perpendicular AP is increasing toward the length OA while point P returns toward 0 where, at θ = 270°, the length of 0P is once again zero.
Finally, as θ increases from 270° to the full rotation of 360°, so OP returns to the value OA and AP returns again to zero; this is shown in diagram (d).
When these four diagrams are compared it is found that always the triangles AOP are mirror images. Thus the ratios sin/cos/tan repeat in value as the angle successively passes multiples of 90° but it must be remembered that, although the numerical values repeat, there are changes of sign to be considered and these are summarised in the following Section.
A full circle is divided into 360° and so, divided by two mutually-perpendicular lines, it contains four right-angles each of 90°; see Fig.6. Each of these quarter-circles are referred to as a quadrant of the circle. In Geometry, Trigonometry and general mathematics it is accepted practice to measure positive distances to the right - starting from a given reference point - and to measure angles in an anticlockwise direction. As shown in Fig. 6 this convention leads to the upper right-hand quadrant being known as the 1st Quadrant, the upper left-hand one as the 2nd Quadrant, the lower left-hand as the 3rd quadrant and the last one as the 4th Quadrant.
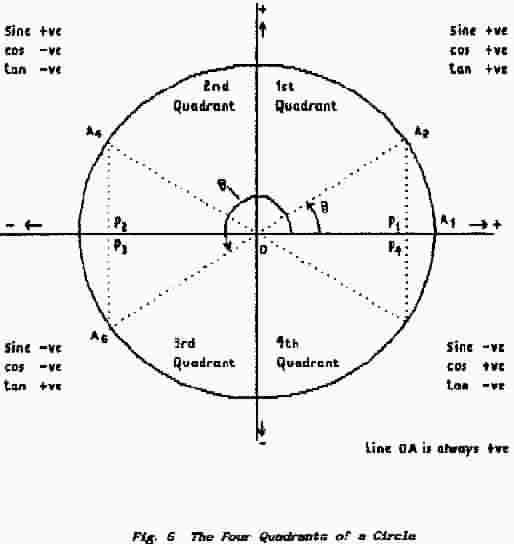
For an angle starting at 0° along OA this horizontal axis always represents the adjacent side and the vertical axis always represents the opposite side (or the perpendicular). It follows that for angles in the first quadrant both adjacent and opposite sides are always positive and so the three ratios also are always positive. For angles in the second quadrant the adjacent side is negative but the opposite side (the perpendicular) remains positive; thus the sine remains positive but the cosine and tangent both become negative in value.
In the third quadrant both the adjacent and the opposite sides are negative and so the sine and cosine are negative but the tangent, the result of dividing one negative quantity by another negative quantity, becomes positive. Finally, in the fourth quadrant, the adjacent side is positive but the opposite side remains negative and so it is the cosine which becomes positive while the sine end tangent stay negative.
Note too that (for example) sinθ = sin(180° - θ )
while cosθ = -cos(180°- θ)
In Fig.7 the upper curve (a) relates to the sine function and begins at θ = 0° when sinθ = 0°; this results because the opposite side has zero length. At 90°, when the hypotenuse and the perpendicular are coincident, the sine ratio reaches a maximum value of 1 and thereafter decreases again toward zero.
The second curve (b) relates to the cosine function and begins at θ = 0 when cosθ = 1; this is because the adjacent side and the hypotenuse are coincident. At 90°, when the adjacent side has zero length, the cosine ratio has fallen to a value of zero and thereafter continues to decrease toward a minimum value of -1.
It has been shown already that the two internal non-right-angles of a triangle are complementary (they sum to 90°) and that the adjacent side for one angle is the opposite side for the other. It should not be surprising therefore that the plot of a sine function yields the same result as the plot for a cosine function but the two curves are displaced by 90°. We say that they differ in phase by 90°.
The third curve (c) is a similar plot for the tangent function and it begins at θ = 0° when tanθ = 0; again this result is caused by the perpendicular having a length of zero. As θ is increased toward 90° so the opposite side increases toward the length of the hypotenuse but, simultaneously, the adjacent side decreases toward zero length. Thus the value of the tangent increases toward a value opposite/zero which has the mathematical value of infinity.
Strictly speaking the value of anything/zero is meaningless but the matter is resolved by the technique of approaching the condition. We say that, as the bottom line approaches zero, so the result approaches an infinite value and it can be written:
as the adjacent side » 0 so tanθ » ∞
(read as as adjacent tends to zero so tan θ tends to infinity)
As the angle increases beyond 90° so the adjacent side once more acquires a finite length which steadily increases but with a negative sign; thus the tangent curve disappears upward toward ∞ at 90°, re-appears at -∞, moves upward to cross the zero-line at 180° and then continues upward again toward +∞. at 270°.
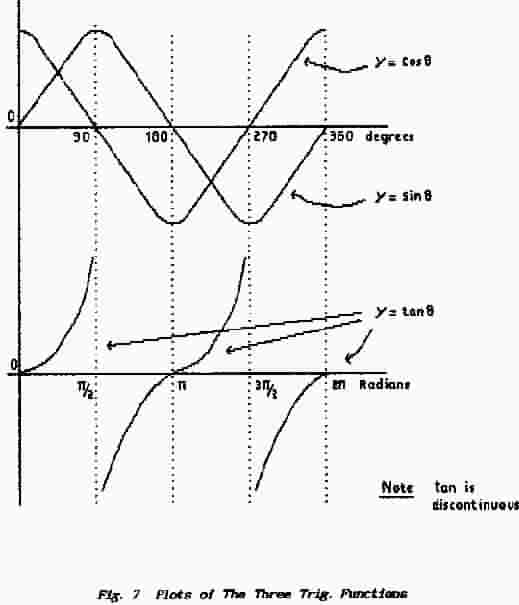
With reference to the sine function:
Peak or Crest values occur at 90° & 270°
Zero Crossings occur at 0°, 180° & 360°
Instantaneous Value constantly changes with Time
Average Value is zero
R.M.S. Value is peak-peak value / √ 2 ( = 0.707 x peak)
As line OA is rotated beyond 360° it clearly is retracing the previous circle and the results can only be the same for trigonometric purposes. However angles greater than 360° do have a significance in electrical-engineering and this is well illustrated by considering the generation of an alternating current by a rotating machine.
Under 1.9.1 Induction (Fundamentals-1, Lesson-4) it was shown that current is induced to flow in a conductor whenever an associated magnetic field changes in value or is moved relative to that conductor. For a conductor to move along a line of magnetic force (a line of constant magnetic strength) does not constitute a change; induction takes place only when motion of the conductor causes it to cross a line of magnetic force. Maximum induction requires that the conductor move at right-angles to the direction of the magnetic lines.
In a rotary generator a coil of wire is spun in a magnetic field as illustrated in Fig.8. Relative motion between conductor and field is such that, at one part of the rotation, the conductor moves parallel with the field while, 90° later, it is moving directly across the direction of the field. Between these two extremes it moves partly along and partly across thc field with the two components constantly changing in a cyclic manner.

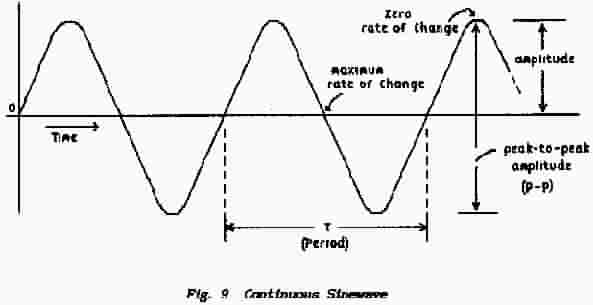
In Fig.8 the line OA drawn from the centre of rotation to the conductor shows the motion of the conductor; it is the same line OA that was drawn in Fig. 5. The induced current is proportional to the motion of the conductor across the field and this is given by the sine of the angle through which the machine has rotated. As the angle of rotation constantly changes so the value of the induced current constantly changes; the current-value at any instant of time is referred to as the instantaneous current and is given by the expression peak-current x sinθ. The machine makes many revolutions per minute and so the angle θ (in theory) becomes very large indeed but the practical result is that the sine function, as plotted in Fig.7 repeats endlessly. The repetitive curve shown in Fig. 9 is known as a sinewave.
The same curve (but mathematically different) that starts from a point of maximum value instead of zero is known as a cosinewave; the difference for a practical engineer is that the two curves are relatively phase-shifted by 90° and are said to be in quadrature.
Both sinewave and cosinewave represent a continually-changing quantity with a cyclic pattern of change. Under steady-state conditions all the positive peaks have the same value, all the negative peaks have the same numerical value and the so-called zero-crossing points - where the curve constantly crosses the horizontal axis - are equally spaced and fall exactly between the positive and negative peaks.
The time required to complete one whole cycle of a waveform is measured between two successive positive crests, between two successive negative crests or, much more accurately, between alternate zero-crossing points. This interval is known as the Period of the wave and usually is assigned the symbol T. This period T is obtained by dividing the number of cycle-per-second (the frequency) into 1 second; hence T = 1/f
Although f represents the number of cycles per second a committee has decreed that frequency shall be expressed in Hertz where
1- Hertz = 1 cycle-per-second.
Where frequency is measured in radians per second the name Hertz is not applied.
The sinewave (or the cosinewave) is the simplest of repetitive waveforms; it is a pure waveform. All other waveforms can be analysed into (or synthesised from) a number of component sinewaves and the process of breaking down a wavetrain into its component sinewaves is known as Fourier Analysis because it was developed by the French Mathematician Fourier.
In repetitive waveforms the components are harmonically related. This means that their frequencies are related by a ratio of whole numbers; i.e. 2 to1, 3 to1, 16 to 1 etc. In any series of such related components the lowest frequency present is termed the Fundamental or sometimes the First Harmonic. If the fundamental is represented by f then a frequency 2f is termed the second harmonic, a frequency of 3f is termed the third harmonic and so on.
Where harmonic frequencies are related also by a factor of two the intervals f - 2f - 4f - 8f etc. are termed octaves. This is a clean and convenient mathematical rule but, in Nature, harmonics are not related by a factor of exactly 2. Two musical notes which, to the ear, sound pleasingly an octave apart prove to be not quite 2:1 in ratio and this is why it is not easy to tune a keyboard instrument or any other musical instrument which uses fixed intervals.
For purposes of calculation an important parameter is the rate at which a waveform changes; for example, in a rotating machine the induced current is proportional to the rate at which the conductor cuts through the magnetic field. With reference to Fig. 5 this is the rate at which the angle θ changes and, expressed in radians, this is 2π f radians per second (2π is one whole cycle and f is the number of cycles per second). This combination is often referred to as the angular velocity and it occurs so often in electrical calculations and expressions that it is represented by the Greek letter ω (omega). Thus the angle swept out by the rotating line OA in a time t is given by ωt radians (the angular velocity in radians/second x time in seconds).
When a waveform is analysed into its constituent components thc result is a set of frequency-components each of which is distinguished by its individual amplitude and also by its phase relation (its time-displacement) with respect to the fundamental. It appears however that the ear is not particularly sensitive to phase relations. The ear finds odd-order harmonics (3rd, 5th, etc) much more objectionable than even-order harmonics and this is the reason that triode valves were favoured in audio amplifiers over pentodes; the triode amplifier tended to produce only even-order harmonics while the pentode amplifier produced mainly odd-order harmonics.
By suitably constructing diagrams that can be broken down into inter-related sets of right-angle triangles it is possible to produce algebraic formulae for combinations of angles such as the sum sinA + sinB(where A and B are angles) and for the product sinA.sinB. Such work is beyond the scope of this Course but the idea is introduced because it has an important bearing on the matters discussed in Fundamentals-2 under Frequency Translation/Multiplication and also under Superheterodyne Receivers.
A complete set of these formulae can be found in electrical and mathematical reference books. The two given below answer the question: " What happens when two or more sinewaves are mixed in the same circuit?" The two formulae are:
(i)
sinA + sinB = 2.sin½(A + B).cos½(A - B)
This indicates that, if you put two different frequencies A and B into a linear (a non-distorting) circuit, they add together to give two different frequencies one of which is (A + B) and the other (A- B). The expression also says that one of these (A + B) in a sine function while the other is a cosine function; that means that they are in quadrature - shifted in phase by 90° relative to each other.
(ii)
sinA.sinB = ½(cosA-B) - ½(cosA + B)
This indicates that, it you put two different frequencies A and B into a non-linear (a distorting) circuit, they are multiplied together to give two different frequencies one of which is (A + B) and the other (A - B). The expression also says that both are cosine functions which indicates that they are in phase.
Both formulae show that, if you wish a circuit to handle a mixture of frequencies in this way, then it must possess a bandwidth that extends (not from A to B) but from (A - B) to (A + B). The newly-generated sum and difference frequencies are known as side frequencies which are dealt with under Transmitters and Receivers in Fundamentals-2.
Back to Top of PageEND OF LESSON